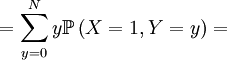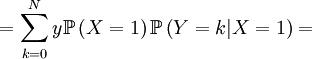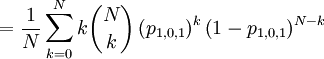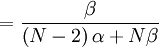Price 3.0
From Evolution and Games
(→A B mutant in a population of A's) |
(→A B mutant in a population of A's) |
||
| Line 106: | Line 106: | ||
p_{1,0,N-1}=\frac{\beta }{\left( N-2\right) \alpha +N\beta } | p_{1,0,N-1}=\frac{\beta }{\left( N-2\right) \alpha +N\beta } | ||
</math> | </math> | ||
| + | |||
| + | So... | ||
| + | |||
| + | <math>\mathbb{P}\left( Y=k|X=0\right) =\binom{N}{k}\left( p_{0,1,N-1}\right)^{k}\left( 1-p_{0,1,N-1}\right) ^{N-k}=</math> | ||
| + | |||
| + | <math>\mathbb{P}\left( Y=k|X=1\right) =\frac{1}{N-1}\binom{N}{k}\left(p_{1,0,N-1}\right) ^{k}\left( 1-p_{1,0,N-1}\right) ^{N-k}+\frac{N-2}{N-1}\binom{N}{k}\left( p_{1,1,N-1}\right) ^{k}\left( 1-p_{1,1,N-1}\right) ^{N-k}</math> | ||
| + | |||
| + | |||
| + | This is pretty well defined, so we can also compute the covariance of these two actual random variables. Let us start with the expectations... | ||
Revision as of 21:53, 18 September 2010
A model with frequency dependence
We go back to the asexual model, but now we will take a model with frequency dependence. This will be a bit more complicated, but we can still use a basic, well known model. Suppose there are $N$ individuals. They are paired randomly, and play a game in those pairs. The game gives them payoffs according to the following payoff matrix
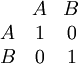
If qi = 1, then that means that individual $i$ plays strategy A, and qi = 0 means that individual i plays strategy B. Depending on the match, each individual gets a payoff πi. The next generation is drawn, as before, one individual at a time. But now the probability that i is drawn as a parent depends on the payoff, and not just on the own genotype.
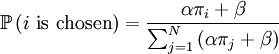
We do the same procedure as before, but with a few different starting points.
An A mutant in a population of B's
Suppose q1 = 1 and qi = 0 for i = 2,...,N. The probability of any individual i = 2,...,N to be matched with individual 1 is 1 / (N − 1).
The probability with which an individual i with qi = 1, who is matched to an individual j with qj = 0, is chosen is:
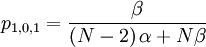
The probability with which an individual i with qi = 0, who is matched to an individual j with qj = 0, is chosen is:
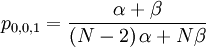
The probability with which an individual i with qi = 0, who is matched to an individual j with qj = 1, is chosen is:
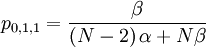
We can also compute the covariance of these two actual random variables. Let us start by computing expectations...
![\mathbb{E}\left[ X\right] =\frac{1}{N}](/wiki/images/math/c/3/8/c389f3bfffa4dec33da0820781e6e99b.png)
For symmetry reasons...
![\mathbb{E}\left[ Y\right] =1](/wiki/images/math/f/6/8/f6851309af9717e71df00c1227f0d760.png)
![\mathbb{E}\left[ XY\right] =\frac{\beta }{\left( N-2\right) \alpha +N\beta }](/wiki/images/math/b/c/1/bc1ba1eb3290d07e011aad2aaf8c6036.png)
The Covariance is thus...
![Cov\left( X,Y\right) =\mathbb{E}\left[ XY\right] -\mathbb{E}\left[ X\right] \mathbb{E}\left[ Y\right] =\frac{\beta }{\left( N-2\right) \alpha +N\beta }-\frac{1}{N}](/wiki/images/math/4/5/1/451efdc1824fac07a0b1bf56a8167a29.png)
A B mutant in a population of A's
Suppose q1 = 0 and qi = 1 for i = 2,...,N. The probability of any individual i = 2,...,N to be matched with individual 1 is 1 / (N − 1).
The probability with which an individual i with qi = 0, who is matched to an individual j with qj = 1...
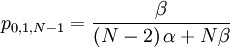
The probability with which an individual i with qi = 1, who is matched to an individual j with qj = 1...
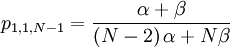
The probability with which an individual i with qi = 1, who is matched to an individual j with qj = 0...
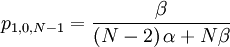
So...
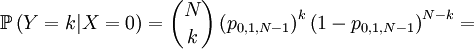
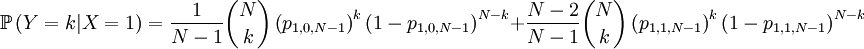
This is pretty well defined, so we can also compute the covariance of these two actual random variables. Let us start with the expectations...
![\mathbb{E}\left[ X\right] =\sum_{x=0,1}x\mathbb{P}\left( X=x\right) =](/wiki/images/math/5/c/8/5c8589cd4e69154ab8f56f7db9f0dc8f.png)
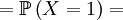
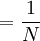
![\mathbb{E}\left[ XY\right] =\sum_{x=0,1}\sum_{y=0}^{N}xy\mathbb{P}\left(X=x,Y=y\right) \text{ (because }xy=0\text{ if either }x=0\text{ or }y=0\text{)}](/wiki/images/math/f/1/4/f146e34f77cefe890894be133473bf2a.png)