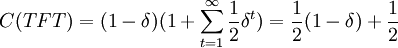Measuring Cooperation and Reciprocity

From Evolution and Games

---

Revision as of 15:12, 22 April 2010

There are two reasons why we would like to have measures for cooperativeness and reciprocity. The first and most important reason is obvious; we would simply like to know how cooperative, and how reciprocal, strategies are during a run. The second reason is that these measures may serve as an indication of indirect invasions. Typically an indirect invasion is characterized by a change in reciprocity followed by a change in cooperativeness.

Any measure of cooperativeness will have to weigh the different histories, and as we will see, every choice how to weigh them has appealing properties and drawbacks. In contrast to the definitions earlier, here it is more natural to look at histories that only reflect what actions the other player has played. This captures all relevant histories for the measurement of cooperativeness, because what a strategy S itself has played is uniquely determined by the history of actions by the other player.

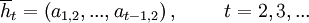
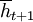Again, we will sometimes also write for a history , and we get the following sets of possible histories at time t.

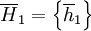
With the repeated prisonners dilemma we have A = C,D, so in that case there are 2^{t − 1} histories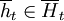

We begin with a measure that tells us how cooperative a strategy is, given that it is facing a history 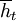. If we weigh a history at time t + s with the probability that the game actually reaches round t + s − 1, given that it has already reached round t − 1, and if we also divide by the number of different histories of length t + s − 1, under the restriction that the first t − 1 rounds of these histories are given by 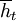, we get the following. Note that this measure does not depend on the environment a strategy is in.

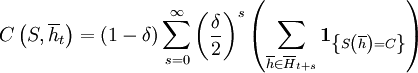
The overall cooperativeness of a strategy S can then be defined as the cooperativeness at the beginning, where we have the empty history; .

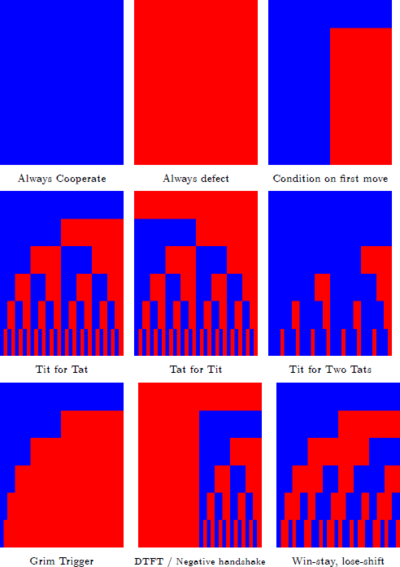
An intuition for what this measure does can be gained from the following figure. The top bar represents the empty history. The second bar represents histories of length 1, and is split in two; the history where the other has cooperated, and the one where the other has defected. The third bar represents histories of lenth 2, and is split in four; the histories CC, CD, DC and DD. This continues indefinitely, but for the pictures we restrict ourselves to histories of length 5 or less. If a part is blue, then that means that the strategy reacts to this history with cooperation, if it is red, then the strategy reacts with defection. Cooperativeness weighs the blueness of those pictures.

It is obvious that C(AllC) = 1 and that C(AllD) = 0. A strategy that starts with cooperation, and further conditions play on the first move entirely has cooperativeness 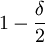. This is sensible; if δ = 0, then the first move is the only move, and since this strategy cooperates on the first move, it should have cooperativeness measure 1. On the other hand, except for the first move, this strategy cooperates in exactly half of the histories of length t for all t > 1. Therefore it makes sense that if δ goes to 1, then cooperativeness goes to .

More simple computations shows that , 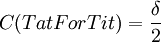and 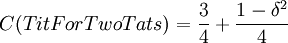. The last simple computation shows that 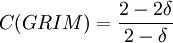, which is 1 at δ = 0 for similar reasons, and goes to 0 if δ goes to 1.