Sociality
From Evolution and Games
This page is under construction, in the meantime please go [here.
The software we provide and describe here reimplements simulations first described in Aviles 2002 using Java . Our simulation program also has alternative fitness functions and some additional features.
Contents |
Editorial Information
van Veelen, Matthijs, Julián García and Leticia Avilés (forthcoming). It takes grouping and cooperation to get sociality. Journal of Theoretical Biology.
Abstract
Cooperation and grouping are regularly studied as separate traits. The evolution of sociality however requires both that individuals get together in groups and that they cooperate within them. Because the level of cooperation can influence selection for group size, and vice versa, it is worth studying how these traits coevolve. Using a generally applicable two-trait optimization approach, we provide analytical solutions for three specific models. These solutions describe how cooperative associations of nonrelatives evolve, and predict how large and how cooperative they will be. The analytical solutions help understand how changes in parameter values, such as the group carrying capacity and the costs of cooperation, affect group size and the level of cooperation in equilibrium. Although the analytical model makes a few simplifying assumptions - populations are assumed to be monomorphic for grouping as well as for cooperative tendencies, and group size is assumed to be deterministic - simulations show that its predictions are matched quite closely by results for settings where these assumptions do not hold.
The genetic system
What individuals are made of
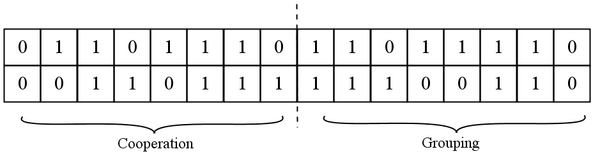
Individuals are characterized by a diploid genome coding for two separate traits; grouping and cooperative tendencies. The number of loci for each of these traits can be chosen by the user of the program. The number of loci for grouping will be denoted by n, and the number of loci for cooperation will be denoted by m. We followed Avilés et al. (2002) by choosing 15 as a default value for the number of loci for both traits. The loci of an individual will be numbered from $1$ to $n+m$, where the first n loci code for grouping tendencies and the loci from n+1 to n+m code for cooperative tendencies. The alleles will be indicated as left and right. At each locus, two alleles (1 or 0) can occur. The tendency of individual i to form groups is denoted by gi, and equals the proportion of 1’s in the grouping portion of its genome, or the number of 1’s divided by 2n. The tendency of individual i to cooperate, denoted by Íi, is the proportion of 1’s in the cooperation part of its genome, or the number of 1’s in the second part of its genome, divided by 2m. This implies that gi and Íi vary between 0 and 1, and are multiples of 1 over twice the number of loci.
The choice for the genome size has an effect on the speed of selection. Reducing the genome size for any one of the tendencies increases the speed of selection for that tendency. This is because the marginal effect of one allele changing from a 0 into a 1 on fitness is larger with a smaller number of loci. The speed of selection of one of the tendencies relative to the other can obviously be tuned by adjusting the one genome size and keeping the other genome size constant.