Price 1.0
From Evolution and Games
| Line 146: | Line 146: | ||
| - | = Confusion = | + | == Confusion == |
The point where confusion starts, is that George Price named the right hand side of this equation ''Cov(z,q)''. The claim of the Price equation - which we contend - is that the equation unveils that a change in frequency - <math>\triangle Q</math> - is explained by the covariance between having the gene and the number of offspring - ''Cov(z,q)''. The central issue here is that this ''Cov(z,q)'' is discussed as if it were a real covariance. Is that correct? | The point where confusion starts, is that George Price named the right hand side of this equation ''Cov(z,q)''. The claim of the Price equation - which we contend - is that the equation unveils that a change in frequency - <math>\triangle Q</math> - is explained by the covariance between having the gene and the number of offspring - ''Cov(z,q)''. The central issue here is that this ''Cov(z,q)'' is discussed as if it were a real covariance. Is that correct? | ||
Revision as of 13:14, 18 September 2010
First model is the simplest...
Intro
Suppose that we have a population of 2 individuals. We depart from a population in which individual no 1 has "the" gene, while the other, individual no 2, does not. In Price equation terms, that means that the variable qi, which denotes the frequency of the gene in individual i becomes: q1 = 1, q2 = 0.
The next generation of 2 individuals is drawn in a very simple way. First we draw the first, and then we draw the second. That makes it - for those who care - a Wright-Fisher process. At both draws the new individual could be the offspring of individual no 1 or of individual no 2. Reproduction is asexual, hence the offspring is a perfect copy of its parent. Now here comes the important thing. We assume that at both draws, the probability of no 1 from the parent population -- the one with the gene -- to be drawn for reproduction is p, while the probability of no 2 from the parent population -- the one without the gene -- to be drawn for reproduction is 1 − p. That gives us four possible transitions.
What the new generation will be is a random variable. What the current generation is, is not; the current generation is simply given. We can however think of a hypothetical chance experiment such that, in combination with the actual random transition, we get two random variables, between which we can define a covariance. So here is the recipe.
1) Draw one of the individuals from the parent population (this is the hypothetical random variable).
2) Draw the next generation (this is the actual random thing that happens in the the transition).
The random variable X is now defined as the genotype of the parent. That is a simple, albeit hypothetical random variable:
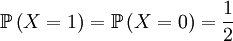 .
.
Then we define the random variable Y, which is the number of offspring that the parent that has been drawn begets. This is a slightly more complicated random variable, because the chances depend on which of the two the (candidate) parent is. So we get a (not too long) list of conditional probabilities. Worth working through!
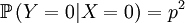
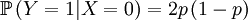
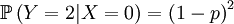
The other conditional probabilities are the reverse,because the parent of a new individual is the one if it is not the other, and vice versa...
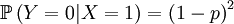
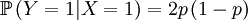

The X and Y are pretty well defined, so we can also compute the covariance of these two actual random variables...
Let us first look at expectations...
![{E}\left[ X\right]=\frac{1}{2}](/wiki/images/math/5/3/c/53ca4d829ebdfac56b0a4a795b3fdb6b.png)
For obvious symmetry reasons; the total number of offspring is 2, and either one could be the parent, so ...
![\mathbb{E}\left[ Y\right] =1](/wiki/images/math/f/6/8/f6851309af9717e71df00c1227f0d760.png)
And ...
![\mathbb{E}\left[ XY\right] = p](/wiki/images/math/0/b/0/0b0cae3e6fa6d5a915323e22d6dc0e86.png)
The covariance is then...
![Cov\left( X,Y\right) =\mathbb{E}\left[ XY\right] -\mathbb{E}\left[ X\right]
\mathbb{E}\left[ Y\right] =p-\frac{1}{2}\cdot 1=p-\frac{1}{2}](/wiki/images/math/9/5/9/95972491d6444efd4a65da33c0d6b4bc.png)
The Price equation for this very simple model
An interesting question would be: is it good to have the gene?
Or, if we do statistics: suppose we know that the process has this form, but we don't know the value of p. Then the question becomes: is p>1/2, or, equivalently, is Cov( X,Y) >0. Below we will try to answer that question. But first we will look at what the Price equation does to all of this.
For a given transition, the Price equation constitutes an identity. The frequency of the gene in the parent population is, in general, defined as
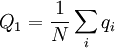
where N is the number of individuals, and qi is the frequency of the gene in individual i (For this particular model this quantity is 0.5).
The frequency of the gene in the offspring population is
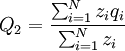
where zi is the number of times individual i in the parent population was drawn for reproduction. The Price equation 1.0 then is the following identity:
![\triangle Q=Q_{2}-Q_{1}=\frac{N}{\sum_{i}z_{i}}\left[ \frac{\sum_{i}z_{i}q_{i}}{N}-\left( \frac{\sum_{i}z_{i}}{N}\right) \left( \frac{\sum_{i}q_{i}}{N}\right) \right]](/wiki/images/math/4/4/f/44f8e6f5c4948ff8a33f39ac612ebe80.png)
In this simple case for N = 2 this amounts to
![\triangle Q=\left[ \frac{\sum_{i}z_{i}q_{i}}{2}-\frac{\sum_{i}q_{i}}{2}\right]](/wiki/images/math/c/a/5/ca5d82021f0f9888efe52c553365e922.png)
Confusion
The point where confusion starts, is that George Price named the right hand side of this equation Cov(z,q). The claim of the Price equation - which we contend - is that the equation unveils that a change in frequency - 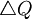 - is explained by the covariance between having the gene and the number of offspring - Cov(z,q). The central issue here is that this Cov(z,q) is discussed as if it were a real covariance. Is that correct?
- is explained by the covariance between having the gene and the number of offspring - Cov(z,q). The central issue here is that this Cov(z,q) is discussed as if it were a real covariance. Is that correct?
Try yourself!
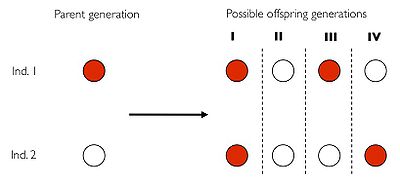
If you tried a few times, you may have found out that 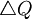 can attain different values; the next generation is a random draw, which implies that the frequency Q can go up by 1/2, remain what it is, or go down by 1/2. The value of this so-called Covariance just follows that change in frequency (and because it is not a real covariance, we will use quotation marks from now on). This creates an illusion of understanding, because whatever happens, the covariance changes along with the outcome of the chance experiment. In other words: the data explain the data.
can attain different values; the next generation is a random draw, which implies that the frequency Q can go up by 1/2, remain what it is, or go down by 1/2. The value of this so-called Covariance just follows that change in frequency (and because it is not a real covariance, we will use quotation marks from now on). This creates an illusion of understanding, because whatever happens, the covariance changes along with the outcome of the chance experiment. In other words: the data explain the data.
This is, of course, not OK; the true and well-defined covariance is

This does not depend on the realisation. Cov(X,Y) defines the properties of the chance experiment, and the realisation of this chance experiment defines "Cov(z,q)".
![\mathbb{E}\left[ X\right] =\sum_{x=0,1}x\mathbb{P}\left( X=x\right) =\mathbb{P}\left( X=1\right) =\frac{1}{2}](/wiki/images/math/2/c/4/2c401f701d21b6b828ae3df887a7c269.png)
![\mathbb{E}\left[ Y\right] =\sum_{x=0,1}\sum_{y=0,1,2}y\mathbb{P}\left( X=x,Y=y\right) =](/wiki/images/math/f/7/4/f74d9e52b468ce85048f50db01ed34ea.png)
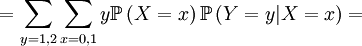
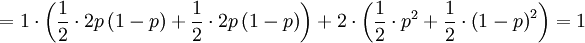
![\mathbb{E}\left[ XY\right] =\sum_{x=0,1}\sum_{y=0,1,2}xy\mathbb{P}\left( X=x,Y=y\right)](/wiki/images/math/d/0/5/d0544224643e3e37b045d33c37858acf.png)

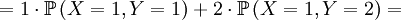
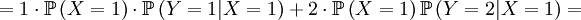
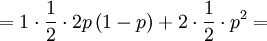

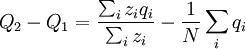
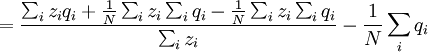
![=N\left[ \frac{\frac{1}{N}\sum_{i}z_{i}q_{i}-\left( \frac{1}{N}\sum_{i}z_{i}\right) \left( \frac{1}{N}\sum_{i}q_{i}\right) }{\sum_{i}z_{i}}\right]](/wiki/images/math/7/2/5/72542d3492ab16325a77c4dc68060bb9.png)
![=\frac{N}{\sum_{i}z_{i}}\left[ \frac{\sum_{i}z_{i}q_{i}}{N}-\left( \frac{\sum_{i}z_{i}}{N}\right) \left( \frac{\sum_{i}q_{i}}{N}\right) \right]](/wiki/images/math/9/5/1/9519ee3f6ad0f358a7a00ccce05fcd78.png)
